使用部品

ＣＭＯＳ　ＩＣ７４ＨＣ００（ＮＡＮＤ）１個

　あるいは７４ＨＣ１３２（シュミットトリガＮＡＮＤ）

ＩＣソケットＤＩＰ１４ｐｉｎ１個

コンデンサ１０００ｐＦフィルム４個

コンデンサ０．１μＦフィルム１個

コンデンサ０．１μＦセラミック（パスコン用）１個

インダクタ１０ｍＨ鉄心入り（空芯不可）２個

固定抵抗１０ｋΩ１／４Ｗ２個

固定抵抗２２０Ω１／４Ｗ１個

ボリューム１０ｋΩ（Ａ型推奨、なければＢ型も可）１個

基板１枚

スペーサ１０ｍｍ以上で同じ長さのもの４個

ＡＣアダプタＤＣ５Ｖ・１Ａ程度（本回路用）１個

ＡＣアダプタ用プラグメス１個

スピーカー８Ω１０Ｗ程度１個

パワーアンプ１０Ｗ以上１個

　※ここでは秋月の「モノラルパワーアンプキット（三洋　ＬＡ４９０２）１０Ｗ」を使用。

　これに付随して以下のものが必要。

　ＡＣアダプタＤＣ１２Ｖ・１．５Ａ以上１個

　ＡＣアダプタ用プラグメス１個

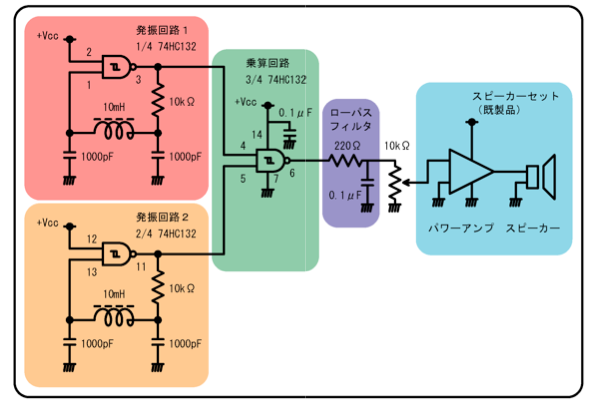
    この装置は２００８年１０月２４〜２５日に行なわれた本研究所の一般公開で当研究室の展示「磁石のしくみ」の中で「磁石で音の変わるおもちゃ」というコンセプトで作製された展示物です。スピーカー接続用のパワーアンプを除く基本回路は、凡用ロジックＣＭＯＳ（７４ＨＣ００あるいは７４ＨＣ１３２）１個がアクティブ素子として発振／ミキサのすべてをまかないます。

    発振源には鉄心入りのインダクタを用いたＬＣ発振回路を使います。インダクタに磁石を近づけると透磁率が変化してそれに応じてＬが変化し発振周波数が変わる仕組みです。ここまではありきたりの話ですが、「ＬＣ発振回路は高周波用であって人間の可聴帯域（２０Ｈｚ〜２０ｋＨｚ）での発振は難しい」という点が問題です。実際に可聴帯域の振動になるようなパラメータを選んで試作をしてみましたが、音は鳴るものの磁石を近づけても発振周波数はほとんど変化しませんでした。これは、コイルが（周波数が低いために）ＬとしてではなくＲ（長い銅線の抵抗）として機能していて実質的にＣＲ発振回路となっているからではないかと私は考えています。そこで次に考えたのは、２つの等価なＬＣ発振回路を作ってそれぞれ独立に発振させて、ミキサを使い両者の周波数の差をとる方式です。俗に言うテルミンはここでＬＣ発振回路の代わりにＣＲ発振回路を使った楽器で、手を近づけるとＣが僅かに変化します。しかし元の発振周波数を高くしているので、周波数の差をとると大きな音程の変化となって現れます。我々の回路では片方のＬＣ発振回路のインダクタに磁石を近づけると音が変わります。これが磁気テルミンたるゆえんです。

    実際の発振回路にはＣＭＯＳインバータ素子を使ったコルピッツ型ＬＣ発振回路を採用しました。（引用元；ＣＱ出版社「トランジスタ技術ＳＰＥＣＩＡＬ　ＯＰアンプによる実用回路設計　馬場清太郎著」ｐ２８１　図２２−４）この回路はディスクリートのトランジスタやＯＰアンプを使った場合にくらべ素子の数が少なくて済みます。とりわけ磁石に感応するはずのインダクタが１個であることが話を簡単にします。難点は出力波形がＯＮ・ＯＦＦの矩形波であることですが、音として認識するためには波形が奇麗な正弦波である必要はないのでこれで充分でしょう。

    ミキサには当初ダブルバランスドミキサを使っていましたが、これは入力段にアンプがないとドライブ出来ないのでアナログ乗算器ＡＤ６３３ＪＮ（アナログデバイセズ）に切り替えました。これでもうまくゆくのですがしかしよく考えると、発振器の出力はＯＮ・ＯＦＦだけなので乗算はＯＦＦ×ＯＦＦ＝ＯＦＦ、ＯＦＦ×ＯＮ＝ＯＦＦ、ＯＮ×ＯＦＦ＝ＯＦＦ、ＯＮ×ＯＮ＝ＯＮの４通りしかありません。これはＡＮＤに相当します。しかも入力や出力が反転していても人間の耳には関係無いので、ド・モルガンの定理によりミキサにはＡＮＤ・ＮＡＮＤ・ＯＲ・ＮＯＲ素子のどれでも使えることが判ります。ここではＮＡＮＤの７４ＨＣ００（あるいはシュミットトリガ型ＮＡＮＤの７４ＨＣ１３２）を採用することにしました。その心は、ＮＡＮＤとしてミキサに使え、また片側の入力を常時ＯＮにすることによりＮＯＴとして発振器に使えるためです。（引用元；ＣＱ出版社「トラ技ＯＲＩＧＩＡＬ　Ｎｏ．２」ｐ２９　図６）これで、必要なアクティブ素子を凡用ロジックＣＭＯＳパッケージ１個に収める事が出来ました。

    磁石を近づけない状態での２つの発振器の出力周波数の実測値はそれぞれ７０．３ｋＨｚと７０．０ｋＨｚでした。２つのインダクタ間の距離は目安として５ｃｍ以上離した方がよいでしょう。近すぎると一方が発生する交流磁界がもう片方に影響を及ぼし発振周期がシンクロしてしまいます。ミキサを通したあとの信号は１４０．３ｋＨｚと（ＤＣ成分があるので）７０．３ｋＨｚ、７０．０ｋＨｚ、０．３ｋＨｚ（およびこれらの高調波）等々の振動の重ね合わせになっていた筈です。このうち０．３ｋＨｚの振動が我々の耳に聞こえる訳です。実際の信号はＯＮ・ＯＦＦの矩形波でＰＷＭ変調になっています。高周波側の振動は放っておいてもどのみち人間の耳には聞こえない（参照元；「トランジスタ技術２００８年３月号」ｐ１３６〜１３７）のでローパスフィルタを入れなくとも低周波側だけが聞こえます。しかしパワーアンプの保護のためにもＣＲ型のローパスフィルタを入れておく方が良いでしょう。

    ローパスフィルタを通した波形をオシロスコープで見ると０．３ｋＨｚの三角波が見えます。矩形波と矩形波を掛け合わせて三角波が出てくる理屈は少々複雑ですがフーリエ級数展開を用いると理解できます。角振動数ω１の矩形波Ｖ１（ｔ）と角振動数ω１＋Δω　（Δω＜＜ω１）の矩形波Ｖ２（ｔ）はそれぞれ

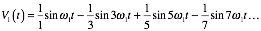
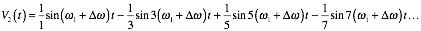
ですが、Ｖ１（ｔ）とＶ２（ｔ）の積を三角関数の積の公式を使って展開したものののうち低周波側の角振動数成分ω≈ｎΔω＜＜ω１（ｎ＝１，２，３．．．）の項を集めたものをＶｏｕｔ（ｔ）とすると、

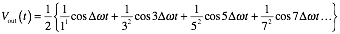
となります。これは三角波のフーリエ級数展開に相当します。理屈はともかく矩形波よりも三角波の方が実際に聞いてみて耳障りが良いようです。

    パワーアンプは何でもよいのですが、秋月の「モノラルパワーアンプキット（三洋　ＬＡ４９０２）１０Ｗ」を使いました。これは片側１２Ｖ電源で動くので電源数が少なくて済みます。システム全体の電源数は５Ｖと１２ＶのＡＣアダプタ計２個で済みました。スピーカーは８Ω１０Ｗのものです。あるいは、パソコンを買ったときに付いてくるスピーカーを使うとアンプが内蔵されていて簡単になると思われます。

    最終的な回路を図に示します。実際に出来上がった回路のインダクタに磁石を近づけてみると音程が変わるのが良く判ります。また磁石に限らず金属を近づけただけでも音が変わります。もっと工夫すれば金属探知器としても使えそうです。２つ発振器の発振周波数が違うので最初から音が出ていますが、あらかじめ別な金属を片方のインダクタに近づけておけば出力周波数を可聴帯域の下に調整することも可能です。完成したものが楽器として実用的かどうかは判りませんが、榊原先生はこれを使ってエーデルワイス（らしき？曲）を演奏しました。