
Last updated: Apr. 14, 2010
◆◆ 回転磁場下の比熱測定による異方的超伝導体のギャップ対称性の研究 ◆◆
s波超伝導体が等方的に開いた超伝導ギャップを持つのに対して、 異方的超伝導体ではある運動量方向に対してギャップがゼロになるノードを一般に持ちます。 ノードには点状のものと線状のものがあり、 その有無は超伝導状態での比熱や熱伝導率、核磁気緩和時間などの温度依存性(低温で温度のべきの関数になる)から推定できます。 一方、超伝導機構を詳しく調べるためにはどの方向にノードが存在するかも重要になりますが、 前記の実験だけでは決まりません。
この「ノード方向を決める」問題は、最近理論・実験ともに急速に進展しつつあります。 基本的なアイデアは以下の通りです。 第二種超伝導体に下部臨界磁場Hc1以上の磁場をかけると渦糸が侵入します(混合状態)。 渦糸の周りには超伝導電流が流れており、その超流体速度vsは磁場と垂直な向きを持ちます。 この運動している超流体からの準粒子励起はドップラーシフトの影響を受けて静止状態と比べて図1のように変化します。
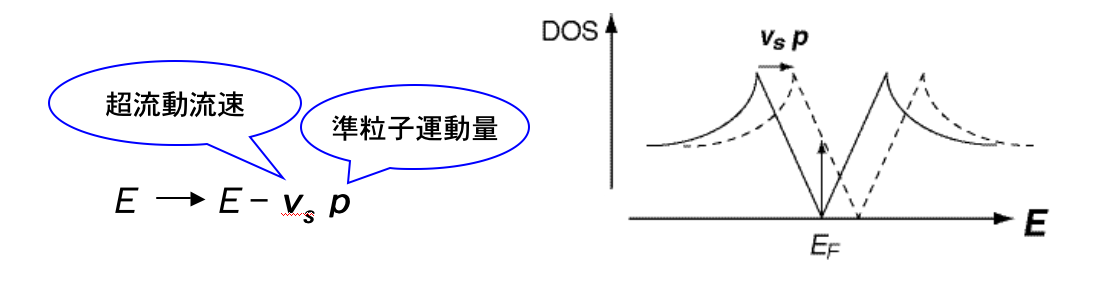
このドップラーシフトの大きさは本来小さいものですが、異方的超伝導の場合、 ノード付近の準粒子に対しては無視出来ない影響を及ぼし、 もともと状態密度のなかったフェルミエネルギーのところに有限の状態密度が現れます。 またドップラー効果はvsと準粒子運動量の内積で決まるので、 ノード近傍の準粒子運動量とvs(すなわち磁場と垂直な向き)との角度の関数として状態密度が変化します。 この角度振動は磁場を回しながら比熱や熱伝導率を測定することで観測することができ、 それらが極小となる磁場方向が一般にノードの方向になります(図2)。
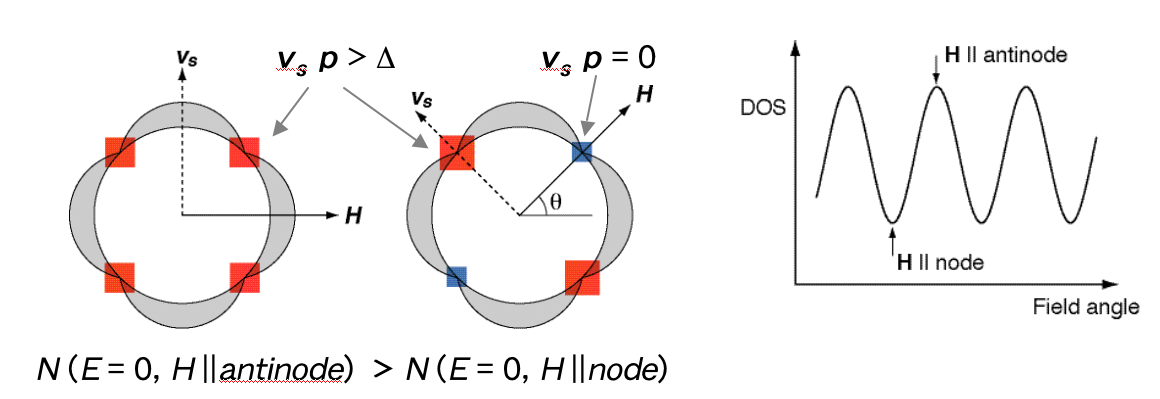
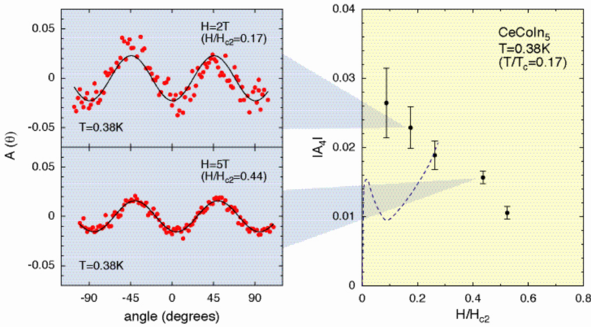
d波超伝導体と考えられているCeCoIn5について、磁場中比熱の磁場回転の実験を行った結果が図3です。 c面内で磁場を回転させると、図のように比熱が4回対称の角度振動することがわかります。 この振動の相対振幅は磁場を2 T(H/Hc2~0.17)に下げても減少する傾向になく、 ノード近傍の準粒子ドップラーシフトによるものであることを強く示唆しています。 すなわち、この系がz方向に走る4回対称のラインノードを持った超伝導体であることを裏付けています(図4)。 また、比熱が[100]方向に極小をとることからギャップ対称性はxy型であることがこの実験からは予想されます。

参考文献
H. Aoki et al.:
J. Phys. Condens. Matter 16 (2004) L13.
最近の結果もご覧ください











