【 Home > 研究内容 > 研究成果 】

Last updated: Apr. 04, 2018

◆◆ 強磁性鎖ベースの梯子鎖を有するフェルダジルラジカル系有機磁性体における量子臨界現象 ◆◆

量子臨界現象とは、絶対零度においてあるパラメータ（磁場等）を動かして相転移が起こる場合（量子相転移）、相転移の起こるパラメータ（量子臨界点、以後QCP）の近傍で種々の物理量が温度のべきに比例するなどの異常が見られることです。 この現象には量子揺らぎが重要な役割を果たしており、QCP近傍でこの揺らぎを介した超伝導や量子スピン液体などエキゾチックな物理が現れる可能性があることから、現代の物性物理において重要なトピックの一つとなっています[1]。

一般的に臨界現象は磁気格子の次元に依存するものの、その格子自体の詳細には依らないという普遍性が知られています。しかしながら、QCP近傍ではフラストレーションの効果などにより、一見本来の格子の次元とは異なる臨界現象が見られる例[2]が報告されています。 このような異常性を検証するには、主たる磁気格子は同一であっても、その相互作用の大きさやフラストレーションの効果が異なる物質群を系統的に研究することが有用だと考えられます。

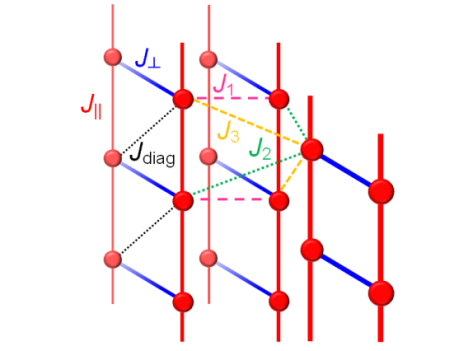
そこで我々が着目したのは、阪府大細越研山口准教授らによって合成された、強磁性鎖ベースの梯子鎖を有するフェルダジルラジカル系有機磁性体3-Br-4-F-V、3-I-V、3-Cl-4-F-Vです。 これらの物質はスピン1/2を持つフェルダジルラジカルをベースとした分子性結晶で、広く実験的研究が行われている反強磁性的な梯子鎖と異なり、足方向が強磁性的(図1のJ_|| < 0)、格方向が反強磁性的(図1のJ_⊥ > 0)な梯子鎖を主要な磁気格子として有しています。 これまでの共同研究[3-6]で3-Br-4-F-Vは格方向が強い(|J_⊥/J_||| > 1)、3-I-Vと3-Cl-4-F-Vは足方向が強い(|J_⊥/J_||| > 1)梯子鎖に分類されることが分かっています。また、これらの物質群は多様な温度-磁場相図を示すことが報告されており、梯子鎖間相互作用(図1のJ₁、J₂、J₃)のフラストレーションがその主たる要因と考えられています。

本研究では、まず主たる磁気格子が同じこれらの物質において、臨界磁場近傍のより詳細な相境界の決定を行いました。その後、相境界の臨界性を特徴づける、べき依存性における臨界指数ν(=1/Φ)を解析し、それら多様な磁気相図のQCPにおける量子臨界現象を調べました。

図1: (画像クリックで拡大)　分子軌道計算から評価された3-Br-4-F-V、3-I-V、3-Cl-4-F-Vの主要なスピン間相互作用による磁気格子の模式図。各赤球は1/2スピンに対応する。

図2(a)に本研究で決定した格方向が強い梯子鎖を有する3-Br-4-F-Vの相境界を示します。比熱(C/T)と磁化率の温度微分(d(Tχ)/dT)に見られる異常から決定しました。強磁性鎖ベースの梯子鎖は理論上、鎖間の相互作用がなければJ_⊥ ≠ 0である限り、スピンギャップを持ちます[7]。これを反映してスピンギャップの閉じる下部臨界磁場H_c1 ~ 4.8 Tと飽和する上部臨界磁場H_c2 ~ 9.2 Tの二つのQCPが相図上に現れます。C/Tとd(Tχ)/dTから決めた転移温度にずれが見られますが、これは試料依存性によるものと考えられます。この相境界の二つのQCP近傍について文献[8]のフィッティング手法を用いて、臨界指数の解析を行いました。 図2(b)に示したのが、臨界指数νのフィッティング幅依存性で、t_maxはフィッティングに用いたデータの上限温度を意味します。この図から試料依存性と測定法による転移温度の定義に依らず、低温に向かってν = 2/3に近づいていく傾向が見られる事が分かりました。

図2: (画像クリックで拡大)　(a) 本研究で定義した3-Br-4-F-VのQCP近傍(H_c1 ~ 4.8 T、H_c2 ~ 9.2 T)の相境界。比熱(C/T)と磁化率の温度微分(d(Tχ)/dT)の異常から決定。白抜き記号は先行研究[4]。相境界が一致しないのは試料依存性のためと考えられる。(b) 相境界の臨界指数νのフィッティング上限温度(t_max)依存性。詳細は本文。点線は三次元BECに普遍的な臨界指数ν = 2/3を示す。

ν = 2/3は三次元のボースアインシュタイン凝縮(BEC)に分類されるQCPに普遍的な臨界指数であり、様々な量子磁性体で観測例があります[2]。しかしながら、これまで強磁性鎖ベースの梯子鎖を有する物質系での検証例はないため、今回の結果は臨界指数が格子の詳細に依らないという普遍性に対応する実験例として意義深いものであると考えられます。本研究成果をまとめた論文はPhysical Review B誌に掲載されました。

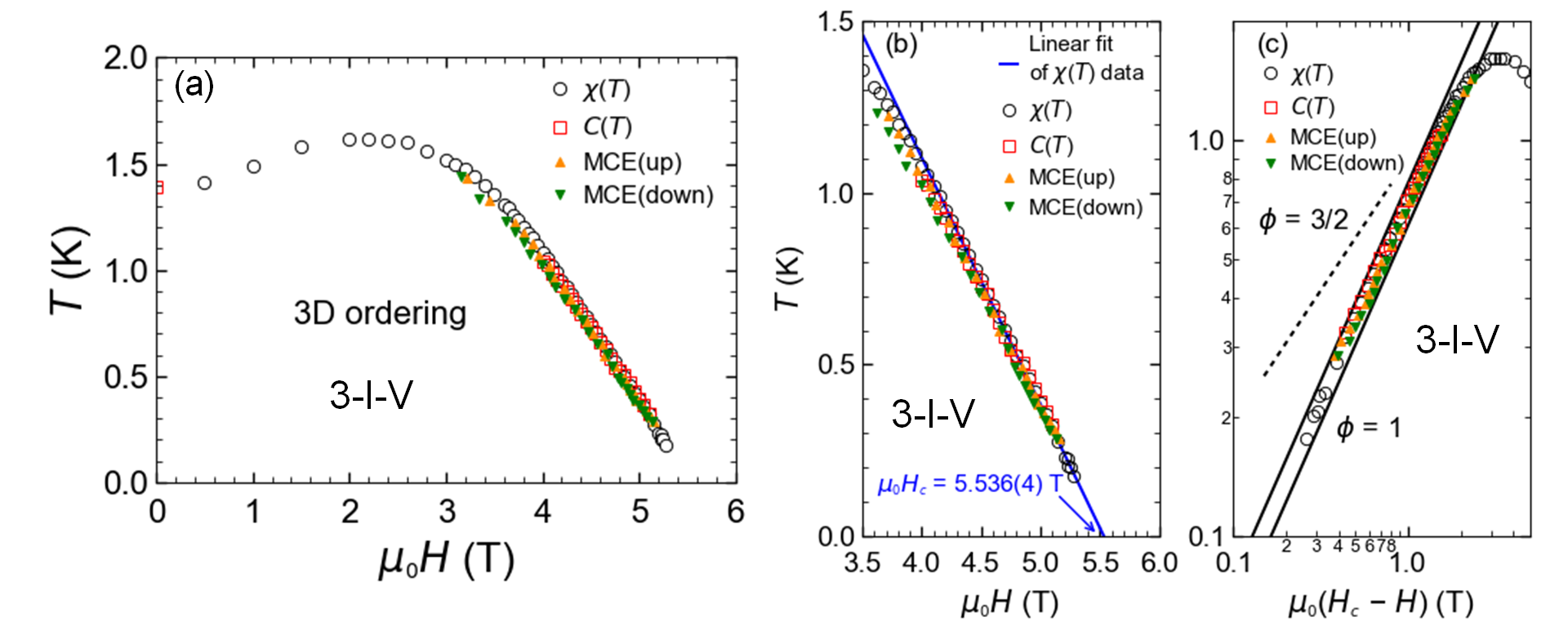
一方で、足方向が強い梯子鎖を有する3-I-Vから得られた飽和磁場近傍の相境界は非従来的な臨界指数の振る舞いを示しました。図3(a)は本研究で決定した3-I-Vの相境界です。磁化率(χ)、比熱(C)に加えて、磁場vs温度相境界の決定について強力な手法である磁気熱量効果(MCE)測定を用いることで、図の様にほぼ完全に一致した定義を得ることに成功しました。 3-I-Vにおいてはスピン間相互作用の違いから、スピンギャップが存在せず、一つのQCP(飽和磁場H_c)のみを持ちます。図3(b)はQCP近傍の相境界の拡大図であり、1 K以下で線形な振る舞いが見られます。ここから線形フィットにより飽和磁場をH_c = 5.536(4) Tと見積もりました。 このH_cを用いて相境界のべき依存性を両対数プロットしたのが図3(c)です。ここから分かるように3-I-VのQCP近傍の臨界指数は測定範囲内では一般的な三次元BECのΦ(=1/ν) = 3/2ではなく、Φ = 1に従っています。

図3: (画像クリックで拡大)　(a) 本研究で定義した3-I-Vの三次元秩序相境界。比熱(C)と磁化率(χ) 及び磁気熱量効果(MCE)を用いて決定。全ての測定法で転移温度の定義はよく一致している。(b) 飽和磁場H_c(QCP)近傍の相境界の拡大図。実線は磁化率の結果の1 K以下に対する線形フィットであり、その外挿からH_c = 5.536(4) Tと見積もった。 (c) H_c - H vs Tの両対数プロット。全データは1 K以下の広い範囲で三次元BECのΦ(=1/ν) = 3/2 (点線) ではなく、Φ = 1 (実線) に従っていることが分かる。

我々はこの臨界指数の起源が擬一次元的なBECに由来していると考えました。文献[9]の理論で弱く反強磁性的に結合した強磁性鎖において、飽和磁場から離れるに従い三次元BECのΦ = 3/2から、擬一次元的性を反映したΦ = 1に臨界指数がクロスオーバーすることが予想されています。 このクロスオーバーが見られる条件は3-I-Vの足方向の強磁性的な相関が強い梯子鎖という条件と類似しており、今回の測定結果はクロスオーバー後の臨界指数を観測したことが期待されます。この擬一次元的なBECの振る舞いはこれまで候補物質がなかったため、本研究はその最初の報告例として重要な成果です。 本研究成果をまとめた論文はPhysical Review B誌にRapid Communicationとして掲載されました。

未出版ですが、残りの3-Cl-4-F-Vについても研究を進めており、こちらも飽和磁場近傍で3-I-Vと同様の相境界の線形性を示しました[10]。格方向が強く、スピンギャップを持つ3-Br-4-F-Vで従来的な三次元BECの臨界性が得られた一方で、足方向が強く、スピンギャップが閉じている3-I-Vと3-Cl-4-F-Vに共通して擬一次元的BECに由来すると考えられる臨界性が見られたことは、 強磁性鎖ベースの梯子鎖を含む量子磁性体の臨界性にある種の普遍性があることを示唆しています。これらの実験結果から、量子磁性体における擬一次元性が量子臨界現象に与える影響への考察がさらに進展することが期待されます。 (河野)

※本研究は大阪府立大学との共同研究です。

[1] S. Sachdev, Quantum Phase Transitions, 2nd ed. (Cambridge Univ. Press, Cambridge, 2011).

[2] V. Zapf et al., Rev. Mod. Phys. 86, 563 (2014).

[3] H. Yamaguchi et al., J. Phys. Soc. Jpn. 83, 033707 (2014).

[4] H. Yamaguchi et al., Phys. Rev. B 89, 220402 (2014).

[5] H. Yamaguchi et al., Phys. Rev. B 91, 125104 (2015).

[6] H. Yamaguchi et al., Phys. Rev. Lett. 110, 157205 (2013).

[7] T. Vekua et al., Phys. Rev. B 67, 064419 (2003); 70, 014425 (2004).

[8] S. E. Sebastian et al., Phys. Rev. B 72, 100404(R) (2005).

[9] A. V. Syromyatnikov, Phys. Rev. B 75, 134421 (2007).

[10] 河野洋平 他、 「スピン1/2有機フェロレッグラダー3-Cl-4-F-Vの量子臨界性」、日本物理学会第73回年次大会(2018).

論文情報

研究リストへ戻る

トップページへ戻る