【 Home > 研究内容 > 研究成果 】

Last updated: Apr. 10, 2015

◆◆ スピン1/2一次元鎖ハイゼンベルク反強磁性体CuPzNにおける磁化の量子臨界的振る舞い ◆◆

スピン1/2一次元鎖ハイゼンベルク反強磁性体は一次元特有の強い量子ゆらぎから現れる朝永ラッティンジャー液体（TLL）と呼ばれる基底状態の特異性や、理論的に厳密解が得られるモデルであることから、 実験と理論の両面から広く研究が行われています[1]。　このモデルでは飽和磁場においてTLLから飽和状態への一種の量子相転移が起こると考えられますが、 一次元性の高い物質として知られるものの多くは飽和磁場が100 T程度の強磁場で、その磁化測定による量子臨界的な振る舞いの詳細な検証は困難でした。

今回、フロリダ大高野教授、クラーク大Landee教授・Turnbull教授のグループから提供いただいた一次元鎖物質の一つであるCuPzNの純良単結晶試料を用いて、キャパシタンス式ファラデー法による高精度な磁化測定を14.7 T、80 mKという高磁場極低温 まで行いました。　CuPzNはCu²⁺上のS=1/2局在スピンがピラジン分子を介して一次元鎖を形成している物質で、その飽和磁場は14 T程度と比較的小さく[2]、今回の測定によって飽和磁場近傍の磁化の量子臨界的振る舞いについて理論との定量的比較を行うことに成功しました。

図1: (画像クリックで拡大)　(a) CuPzNの最低温80 mKにおける磁化曲線（M）及び磁化の磁場微分（dM/dH）（solid symbols）と理論計算（open symbols）の比較。(b) 飽和磁場（H_s=13.97 T）近傍の磁化曲線（赤丸）、80 mKでの理論曲線（四角）、及び絶対零度でのベーテ仮設による厳密解（点線）。測定結果は全磁場領域において定量的によく理論計算と一致している。

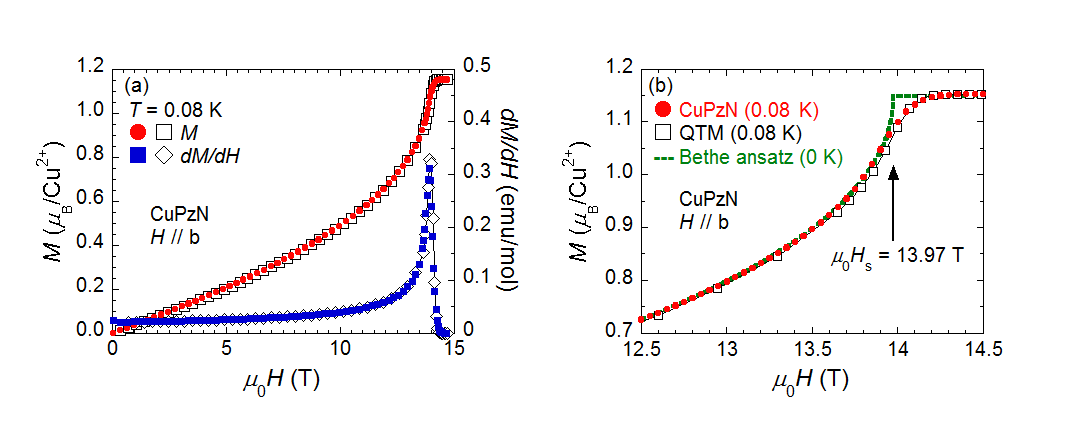
図1に最低温80 mKで得られた磁化曲線と同温度でのスピン1/2一次元反強磁性ハイゼンベルクモデルの磁化の理論計算結果を示します。理論曲線は量子転送行列法（QTM）[3]という手法に基づいて、東大総合文化研究科の堀田知佐准教授に計算していただきました。 実験結果は理論曲線と飽和磁場まで定量的に良い一致を示しており、CuPzNがこの温度においても理想的な一次元系として扱えることがわかります。絶対零度の厳密解を与えるベーテ仮設法による磁化曲線[4]との比較から、飽和磁場をH_s = 13.97 Tと見積もりました。

図2: (画像クリックで拡大)　(a) H_sのほぼ直上14 Tにおける磁化の温度依存性（白丸）、及び理論計算結果（十字）。その量子臨界的な振る舞いが~T^1/2のべきでよくフィッティングできる（青線）。(b) H_s近傍、種々の磁場下での 磁化の温度依存性。ブロードなピークの位置（T_p）を矢印で示した。　(c) 磁化の温度微分から得られた等高線プロットによるCuPzNの磁気相図。磁化の温度依存性に見られたブロードピークの位置（T_p）を白丸で示す。点線は理論から予測される磁化が極値を持つ温度の漸近線。

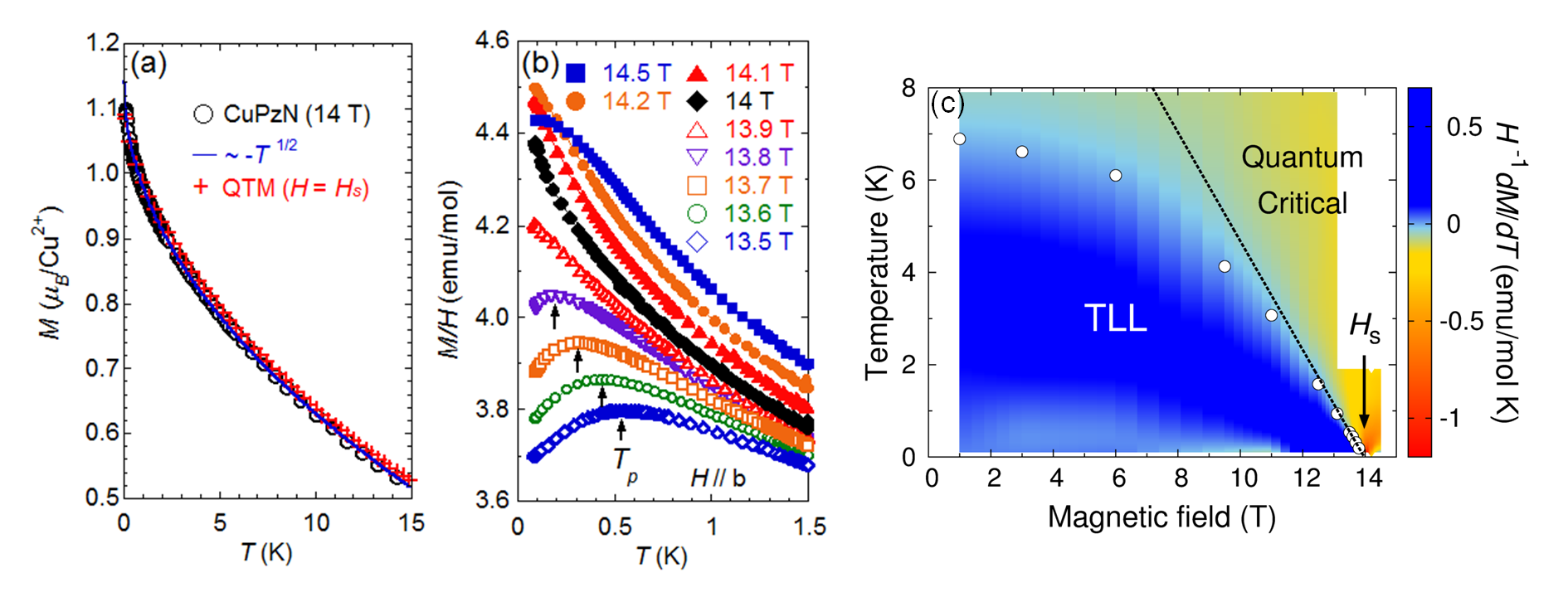
図2(a)に示したのは上述したH_sのほぼ直上14 Tにおける磁化の温度依存性で、最低温80 mKまで理論計算とよく一致しているだけでなく、その振る舞いが~T^1/2のべきでよくフィッティングできることがわかります。このような磁化の温度に対するべき依存性はH_sにおける量子臨界性を示しています。一方、H_sから磁場を下げていくと図2(b)に示したようにブロードなピークが現れ、これはTLLから常磁性領域へのcrossover温度の目安と考えられます。 これらの結果から得られたCuPzNの磁気相図を図2(c)に示しました。白丸は前述の各磁場下でのブロードなピークの温度（T_p）を表しています。

今回、これらH_sにおける量子臨界的振る舞いや、その近傍のT_pの振る舞いについて飽和状態から励起されたマグノンの自由フェルミオン近似[5,6] によって現象論的に説明しました。今の場合、すべてのスピンの向きが揃った飽和状態からマグノンを一つ励起することは全磁化Mを1減少させることに対応し、したがって励起されたマグノンの粒子数と磁化が対応します。 通常マグノンはボース粒子として扱いますが、励起される粒子数が希薄なH_s近傍では相互作用しないフェルミ粒子として近似できることが知られています[5,6]。実際、この近似を元に計算した磁化はH_s直上で~T^1/2のべき依存性を示し、H_sから磁場を下げていくとある温度で極大を持ちます。図2(c)の相図上の点線で示したのが自由フェルミオン近似で磁化が極大を持つ温度です（実際にはマグノンは互いに相互作用するのでH_sから離れると、この直線からはずれます）。 実験で得られたT_pと比較すると、H_sへ漸近する振る舞いがこの直線でよく説明できることがわかります。この直線の傾きは物質のパラメータ （鎖内相互作用J や、g値）によらず決まりますが、今回の測定結果はそのuniversalityを示す一つの実例となりました。

以上のように本研究はCuPzNの理想的な一次元性を示すとともに、スピン1/2一次元反強磁性ハイゼンベルクモデルにおける一種の量子臨界点となっている飽和磁場近傍での磁化の振る舞いについて、初めて実験と理論との定量的比較をおこなった重要な成果です。本研究成果をまとめた論文はPhysical Review Letters誌に掲載されました。

[1] T. Giamarchi, Quantum Physics in One Dimension (Oxford University Press, Oxford, 2004).

[2] P. R. Hammar et al., Phys. Rev. B 59, 1008 (1999).

[3] A. Klümper, Z. Phys B 91, 507 (1993).

[4] R. B. Griffiths, Phys. Rev. 133, A768 (1964).

[5] F. D. M. Haldane, Phys. Rev. Lett. 48, 569 (1982).

[6] Y. Maeda et al., Phys. Rev. Lett. 99, 057205 (2007).

論文情報

研究リストへ戻る

トップページへ戻る