橘高 俊一郎 personal page

角度分解磁場中比熱測定から明らかにしたCeIrIn₅の超伝導ギャップ構造

重い電子系物質CeMIn₅シリーズ（M= Co, Rh, Ir）では量子臨界点近傍で非従来型超伝導が発現し、その対形成発現メカニズムに興味が持たれています。実験と理論の両面からの研究によって、CeCoIn₅はd_x²-y²波超伝導体であることが決定的[1-3]、CeRhIn₅の圧力誘起超伝導もd_x²-y²波[4]であることが広く受け入れられています。しかし、CeIrIn₅（T_c=0.4 K）については、回転磁場中熱伝導率測定[5]から『d_x²-y²波ギャップ』を支持する結果が報告される一方で、熱伝導率の熱流方向に対する異方性[6]からはk_zまたはk_z(k_x+ik_y)という『水平ラインノードを持ったギャップ構造』の可能性が指摘されており、未解決の問題として残されています。そこで、我々はCeIrIn₅の超伝導ギャップ構造の決定を目指して角度分解磁場中比熱測定を80 mKの低温まで行いました。

回転磁場中比熱測定による超伝導ギャップ構造の決定方法の詳細についてはこちらをご覧ください。簡単にご説明しますと、超伝導ギャップにノードが存在すると、磁場をかけた際にそのノード周りで比較的大きな準粒子励起が生じます。この準粒子励起は磁場がノード方向を向いたときに強く抑制されるため、準粒子状態密度を検出可能な比熱を回転磁場中で測定することにより、比熱が極値をとる磁場方向からノード方向を決定することができます（擬2次元超伝導体を想定）。ただし、ノード方向の磁場下で比熱が極大・極小のいずれを示すかは温度と磁場で変化するため、ノード方向の決定には慎重な考察が必要となります[1,3]。

まず、ab面に沿って回転させた磁場中での比熱の変化を図1に示します。比熱は磁場と結晶の[100]方向のなす角（φ）に対して4回対称の振動を示し、110 mK, 0.2 Tでは<100>方向の磁場下で比熱が極小を持つことを明らかにしました。

図1 : 110 mK, 0.2 TにおけるCeIrIn₅のab面内回転磁場中比熱。φは磁場と結晶[100]軸のなす角度。比熱はφに対して4回対称の振動を示し、<110>方向の磁場下で極大を示す。

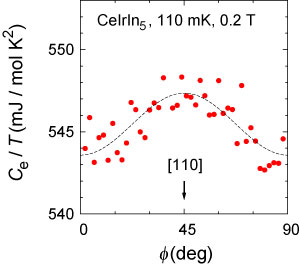
さらに、この4回振動の相対振幅A₄が温度・磁場に対してどのように変化するか調べたところ、図2（左）に示すように0.3T_c, 0.15H_c2付近でピークを持ち、0.2T_cではほぼゼロになることが分かりました。この特徴を微視的理論に基づくA₄の数値計算結果[7]と比較したところ、d_x²-y²波ギャップを仮定した理論計算結果［図2（右）］と非常に良い一致を示し、d_x²-y²波ギャップを支持する結果が得られました。

図2 : 4回対称比熱振動の相対振幅A₄の温度・磁場依存性の（左）実験結果と（右）d_x²-y²波ギャップを仮定した理論計算結果。 A₄が0.3T_c, 0.15H_c2付近でピーク（紫色）を持ち、0.2T_c付近でほぼゼロ（黄緑色）になる点など実験と理論で良い一致が見られる。

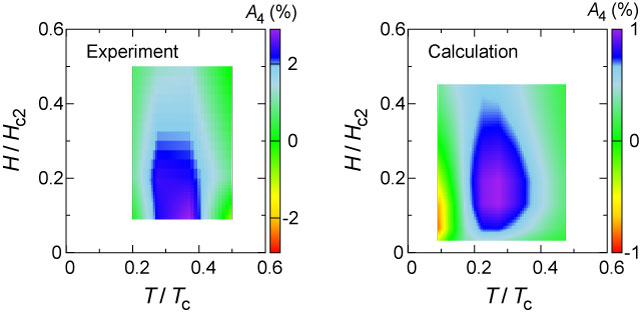
しかし、上述の実験だけでは水平ラインノードギャップの可能性を完全に排除することはできません。水平ラインノードギャップを支持するグループ[6]が主張するように、回転磁場中実験の4回振動はd_x²-y²波でなくても超伝導ギャップの大きさが方位角φに対して4回対称の異方性（ギャップ極小）を持てば説明は可能です。そこで、我々は円錐状に回転させた磁場中比熱測定から水平ラインノードの有無を検証することを試みました。

まず、図3(a)、3(b)にそれぞれ、『水平ラインノード＋ギャップ極小』および『d_x²-y²波』のギャップ構造を想定して計算したA₄の極角θ依存性を示します。d_x²-y²波ではA₄はθとともに単調に減少することが期待されますが、水平ラインノードギャップの場合は対照的にθ=90でA₄が極小を持つことが予想されます。このA₄の極小は、k_z=0に水平ラインノードが存在するため、ab面に沿って磁場を回転させたときに常に（ノードが磁場方向に存在することによる）準粒子励起の抑制が起こり、準粒子励起（比熱）の磁場方位異方性が抑制されたと解釈できます。

図3 : (a)水平ラインノードギャップおよび(b)d_x²-y²波ギャップを想定したA₄の極角θ依存性の数値計算結果。(c)コニカルな回転磁場中比熱測定から得られたA₄のθ依存性の実験結果。水平ラインノードギャップではθ=90でA₄が極小を示すことが期待されるが、実験結果では観測されていない。

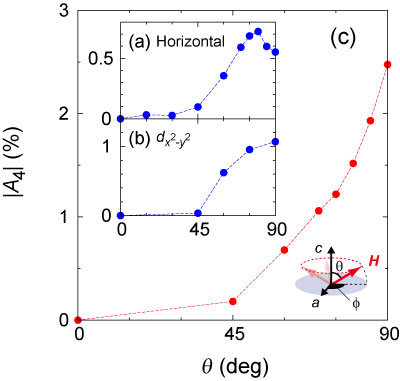
実際に実験を行ったところ、図3(c)のようにA₄はθとともに単調に減少し、d_x²-y²波で期待される振る舞い［図3(b)］と良く一致することが分かりました。一方、水平ラインノードで予想される振る舞い［図3(a)］とは定性的に異なっており、水平ラインノードは存在しないことが明確となりました。以上の結果から、CeIrIn₅はd_x²-y²波超伝導体であると結論づけることができます。

CeCoIn₅、CeRhIn₅と並んでCeIrIn₅でもd_x²-y²波超伝導が確立したことはCeMIn₅系（M=Co, Rh, Ir）における普遍的な対形成機構を物語っており、超伝導発現メカニズムを理解する上で非常に重要な成果です。本論文はPhysical Review B誌のRapid Communicationに掲載され、Editors' suggestion & Physics Synopsisに選ばれました。また、新学術領域研究『重い電子系の形成と秩序化』のNews letter第4巻第2号にも解説記事が掲載されています。

[1] K. An et al., Phys. Rev. Lett. 104, 037002 (2010).

[2] K. Izawa et al., Phys. Rev. Lett. 87, 057002 (2001).

[3] A. B. Vorontsov and I. Vekhter, Phys. Rev. Lett. 96, 237001 (2006).

[4] T. Park et al., Phys. Rev. Lett. 101, 177002 (2008).

[5] Y. Kasawhara et al., Phys. Rev. Lett. 100, 207003 (2008).

[6] H. Shakeripour et al., Phys. Rev. B 82, 184531 (2010).

[7] M. Hiragi et al., J. Phys. Soc. Jpn. 79, 094709 (2010).

論文情報

Recent topics一覧へ戻る